拉奥—夏昆模型

拉奥（Ambar G.Rao）和夏昆(Melvin F.Shakun)于1972年提出了关于新品牌进入市场的价格模型。

拉奥—夏昆模型既充分考虑到了市场结构，又考虑到了在实现价格战略过程中的企业品牌目标和竞争者目标。

拉奥—夏昆模型的推导

拉奥—夏昆模型是建立在如下假设基础上的：

（1）仅考虑同质顾客群体；

（2）顾客群体中某一成员愿意支付的最低价格为呈对数正态分布的随机变量，且均值为μ，方差为δ2；

（3）对每一顾客来说，存在一固定的对数价格尺度，其间距为α，它标志着顾客可接受价格的幅度，顾客群体中某一成员愿意支付的最大高价格也是对数正态分布的随机变量，且均值为（μ+α），方差为δ2。

单一品牌的最优价格公式：

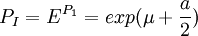
$P_I=E^{P_1}=exp(\mu+\frac{a}{2})$

为研究多品牌市场上有消费者选择行为，拉奥和夏昆又引入了另外的行为假设，主要强调两点：

（1）注重产品质量的顾客群体，占所有顾客的比例为λ，他们在可接受的价格幅度内愿意购买较高价格的品牌；

（2）注重产品价格的顾客群体，占所有顾客的比例为（1-λ），在其可接受的幅度内愿意购买较低价格的品牌。

通过推导可以得出结论：

（1）占所有顾客比例为πj的人不会转向品牌2，因为他们认为P2是个太高的价格，这个比例也就是品牌忠诚细分市场，而

$(\frac{P_2-a-\mu}{\delta})$

（2）如果P1-P2≥a，则这两个品牌不构成竞争关系，因为它们并不分享同一市场上的购买者，在这种情况下，企业可通过市场结构分析，来决定是否引入新品牌来补充现有的品牌系列。

（3）品牌1可通过强调其产品质量而夺走品牌2的某些份额，这是λ值下降的结果，品牌2也可因强调其价廉而夺走品牌1的某些生意。

（4）品牌i的市场占有率Si为：

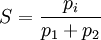
$S=\frac{p_i}{p_1+p_2}$

i=1,2

假定品牌1已占据市场而品牌2试图进入市场。

在竞争条件下的结果是：

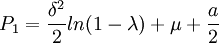
$P_1=\frac{\delta^2}{2}ln(1-\lambda)+\mu+\frac{a}{2}$

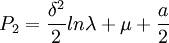
$P_2=\frac{\delta^2}{2}ln\lambda+\mu+\frac{a}{2}$

而当企业采取合作战略（即第三种品牌定价目标）时，市场销售最大化的最优价格分别为

P1=a

P2=μ+a